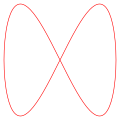
Today worked on an experiment to produce Lissajous figures using two square waves. Wrote Program in python and tested the same. Could obtain various Lissajous patterns.

In the code we used Capture2 function from ExpEYES library to plot the figures. Here is the example…

_________________________________________________________________________

from pylab import *
import expeyes.eyesj
p = expeyes.eyesj.open()
from pylab import *
t1,v1,t2,v2 = p.capture2(1, 2, 300, 100)
figure(1)
plot(t1,v1)
figure(2)
plot(t1,v1, t2,v2)
figure(3)
plot(v1,v2)
show()

__________________________________________________________________________

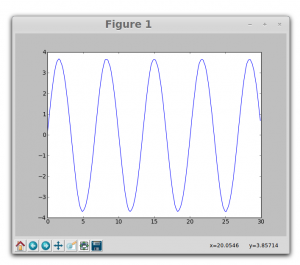
figure 1 is a sine wave connected to channel A1

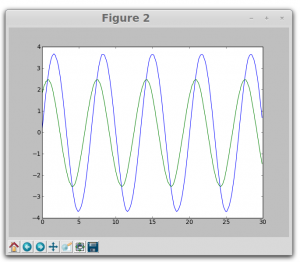
figure2 shows the phase different introduced using a 1 microfarad capacitor and 1kilo ohm resistor.

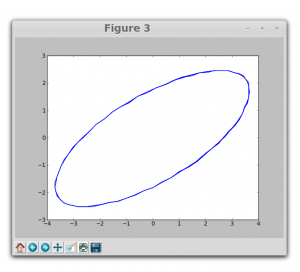
this is the resulting Lissajous pattern…..

Need to create a GUI where user can change the phase between the two waves and can obtain different patterns.

Tomorrow I will be working on the same experiment to produce different patterns.

 Following is the related information

Source :

1. http://www.britannica.com/EBchecked/topic/343305/Lissajous-figure
2. http://en.wikipedia.org/wiki/Lissajous_curve

Lissajous figure, also called Bowditch Curve, pattern produced by the intersection of two sinusoidal curves the axes of which are at right angles to each other.

If the frequency and phase angle of the two curves are identical, the resultant is a straight line lying at 45° (and 225°) to the coordinate axes. If one of the curves is 180° out of phase with respect to the other, another straight line is produced lying 90° away from the line produced where the curves are in phase (i.e., at 135° and 315°).

Otherwise, with identical amplitude and frequency but a varying phase relation, ellipses are formed with varying angular positions, except that a phase difference of 90° (or 270°) produces a circle around the origin. If the curves are out of phase and differing in frequency, intricate meshing figures are formed.

The appearance of the figure is highly sensitive to the ratio a/b. For a ratio of 1, the figure is an ellipse, with special cases including circles (A = B, δ = π/2 radians) and lines (δ = 0). Another simple Lissajous figure is the parabola (a/b = 2, δ = π/4). Other ratios produce more complicated curves, which are closed only if a/b is rational. The visual form of these curves is often suggestive of a three-dimensional knot, and indeed many kinds of knots, including those known as Lissajous knots, project to the plane as Lissajous figures. (REF: http://en.wikipedia.org/wiki/Lissajous_curve)